ia

BLOG INTELIGENCIA ARTIFICIAL SEGUNDO PARCIAL

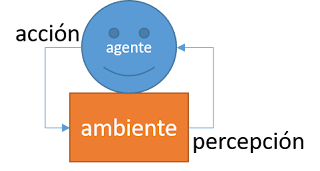
Programación orientada a agentes

Un agente es un sistema computacional capaz de actuar de manera autónoma para satisfacer  sus objetivos y metas, mientras se encuentra situado persistentemente en su medio ambiente.

Ejemplos de entidad puramente virtual serían:

• un software de descubrimiento de patrones en Internet que sólo interactúa con otros software.
• un software softbot que simula a una persona en un juego de computadora, tal como un jugador de ajedrez, un jugador de fútbol contrincante o un conductor de carreras de automóviles, etc.

Es posible clasificar a los agentes inteligentes en 6 categorías principales:

1. agentes reactivos
2. agentes reactivos basados en modelo
3. agentes basados en objetivos
4. agentes basados en utilidad
5. agentes que aprenden
6. agentes de consultas

Agentes para la resolución de problemas

Un agente de este tipo elige un objetivo y trata de satisfacerlo

Algoritmo de busqueda

• Entrada: un problema.
• Salida: secuencia de acciones.

Un problema consta de cuatro soluciones

1. Estado inicial: estado en el que comienza el agente.
2. Descripción de las posibles acciones disponibles por el agente: función sucesor.
3. Test objetivo: determina si el estado es un objetivo.
4. Función de costo del camino: asigna un costo numérico a cada camino.

Una solución de un problema es un camino desde el estado inicial asta un estado inicial

• Su calidad se mide por la función costo camino.
• La solución optima tiene el costo mas pequeño.

Estrategia de busqueda

• Se definen eligiendo de acuerdo a la expansión de nodos.
• Completitud: se encuentra la solución si esta existe.
• Complejidad temporal: numero de nodos generados/expandidos.
• Optimalizad: solución al mas bajo costo.

Arboles de busqueda

Árbol de Búsqueda Binaria

Un árbol de búsqueda binaria es una estructura de datos basada en nodos donde cada nodo contiene una llave y dos subárboles, el izquierdo y el derecho. La complejidad temporal del algoritmo de búsqueda en un árbol de búsqueda binaria es la altura del propio árbol, la cuál es menor que O(log n) para un árbol que contiene n elementos.

B-Tree

La ventaja es que este tipo de árbol no necesitan ser reequilibrado con tanta frecuencia como otros árboles. debido al rango variable de la longitud de sus nodos, los B-trees están pensados para sistemas que leen grandes bloques de datos. También se usan comúnmente en bases de datos.

(a,b)-tree

Un (a,b)-tree es un árbol de búsqueda donde todas sus hojas tienen la misma profundidad. Cada nodo tiene al menos a hijos y a lo sumo b hijos, mientras que la raíz del árbol posee entre 2 y b hijos.

Árbol de búsqueda ternaria

Un árbol de búsqueda ternaria es un tipo de trie que puede tener 3 nodos: un hijo menor, un hijo igual y un hijo mayor. Cada nodo almacena un solo carácter y el árbol en sí se ordena de la misma forma que un árbol de búsqueda binaria, con la excepción de un posible tercer nodo.

Clasificación de problemas

Lógica proposicional

Lógica proposicional

·         La lógica proposicional es la más simple, pero ilustra las ideas básicas.

·         Supone que existen hechos (proposiciones) que pueden darse o no en el mundo, es decir, ser ciertos o falsos.

Lógica proposicional: sintaxis

·         Las sentencias se construyen siguiendo las reglas:

Las constantes y los símbolos proposicionales son sentencias.

Una sentencia entre paréntesis es una sentencia

Si S es una sentencia, ¬ S es una sentencia (negación)

Si S 1 y S 2 son sentencias, S 1 ∧ S 2 es una sentencia (conjunción)

Si S 1 y S 2 son sentencias, S 1 ∨S 2 es una sentencia (disyunción)

Si S 1 y S 2 son sentencias, S 1 ⇒ S 2 es una sentencia (implicación)

Si S 1 y S 2 son sentencias, S 1 ⇔ S 2 es una sentencia (bi-condicional)

·         Existe un orden de precedencia entre los operadores: ￢, ∧, ∨, ⇒ y ⇔

Lógica proposicional: semántica

·         Cada modelo especifica un valor de verdad para cada símbolo proposicional

·         El significado de las conectivas se especifica mediante sus tablas de verdad

P	Q	￢P	P∧Q	P∨Q	P⇒Q	P⇔Q
False False True True	False True False True	True True False False	False False False True	False True True True	True True False True	True False False True

·         Para definir el significado de sentencias más complejas se procede incrementalmente. P.ej.: para definir (P ∨ Q) ∧ ￢S, obtendremos primero el significado de (P ∨ Q) y el de ￢S

Inferencia por tablas de verdad

·         Las tablas de verdad se pueden utilizar como método para comprobar la validez de una sentencia

·         Por ejemplo, para comprobar la validez de

((P∨H) ∧￢H) ⇒ P

P	H	P∨H	(P∨H) ∧￢H	((P∨H) ∧￢H) ⇒P
False False True True	False True False True	False True True True	False False True False	True True True True

Aplicación de reglas de inferencia

·         Patrones de inferencia que se utilizan a menudo y cuya robustez se ha probado. Algunos de los más comunes:

·         Ej.: para probar que P se deriva de (P∨H) y ￢H se debe aplicar la regla de resolución unitaria con P en lugar deαy H en lugar de β

Equivalencia lógica

Bibliografia

https://www.uv.mx/aguerra/documents/2011-sma-01.pdf
https://www.uv.mx/personal/edbenitez/files/2010/09/CursoIA10-II-1.pdf
https://es.wikipedia.org/wiki/Árbol_de_búsqueda
http://inteligenciaartificialgrupo33.blogspot.mx/p/metodos-de-busqueda-y-ejemplos.html
https://www.uv.mx/personal/edbenitez/files/2010/10/CursoIA10-III-2.pdf